内容提要 張家山漢簡《算數書》第143簡算題名稱原整理報告和時賢誤釋爲“鄆都”，後改釋“斬都”，從原簡照片和將此二字與整個張家山漢簡相關文字進行對比，可知改釋是正確的。學界認爲該題的圖形同於《九章算術》中的“芻甍”或“壍堵”的觀點是錯誤的，且學界未能解釋題名“斬都”的詞源意義（得名之由）。都，是個楚方言詞，指“橛”，即“短木樁、木橛子”類義。根據該題給出的條件、結果和算法（術）可知，題名“斬都”，指砍削短木樁、木橛子而成的楔形，並特指砍削木樁而成的楔口向下、楔口的長度大於與之平行的楔座邊的長度的非標準楔形。“斬都”題是江東的學者對嶽麓書院藏秦簡《數》195/0456－196/J13類算題的發展，該題與《九章算術》“羨除”題也具有聯繫，說明“斬都”題淵源有自。

關鍵詞 張家山漢簡《算數書》 鄆都 斬都 楚方言 非標準楔形

一、研究現狀上個世紀80年代初在湖北江陵張家山247號漢墓中發掘出了大批漢簡，其中包括有名的《算數書》。^[1]《文物》於2000年第9期發表了江陵張家山漢簡整理小組《江陵張家山漢簡〈算數書〉釋文》，和彭浩《中國最早的數學著作〈算數書〉》，^[2]文物出版社於2001年11月刊佈了其整理報告。^[3]同年7月，該批漢簡的主要整理者之一同時也是《算數書》的主要整理者彭浩，在科學出版社出版了《張家山漢簡〈算數書〉注釋》（以下簡稱“彭書”），該書是《算數書》整理研究成果中影響最大的專著，因爲該書不光對《算數書》給予了詳細注釋，並且還系統地給出了各題的演算法，若是幾何題，還繪出了該題的幾何圖形。自《江陵張家山漢簡〈算數書〉釋文》發表之後，學界對《算數書》的釋讀展開了不少研究，產生了不少成果。但是，儘管《算數書》的研究已近20年，而包括整理報告在內的時賢對《算數書》第143簡算題的解讀還存在一些問題，很有必要繼續研究予以補正。

第143簡共44字，內容是一道完整的幾何算題，即開始稱之爲“鄆都”後來改稱“斬都”的算題。該簡整理報告的釋文及注釋如下：

鄆都 鄆都下厚四尺，上厚二尺，高五尺，袤二丈，責（積）百卅（三十）三尺少半尺。术（術）曰：倍上厚，以下厚增之，以高及袤乘之，六成一。

整理小組注：“鄆都：疑讀作‘壍堵’，據簡文所述可知，其上底是一矩形，下底是一楔形，並不同于《九章算術·商功》的‘壍堵’，而與‘芻甍’形同。”^[4]

彭浩《張家山漢簡〈算數書〉注釋》的釋文與整理報告基本相同，祗是“術（術）曰”前是逗號而已。彭書的注釋也與整理報告基本相同，該書注曰：

鄆都，疑讀作“壍堵”。據簡文所述可知，其上底是一矩形、下底是一綫段的楔形（見下圖），並不同于《九章算術》商功章的“壍堵”，而與“芻甍”形同。^[5]

彭浩《中國最早的數學著作〈算數書〉》（簡體排印）說^[6]：

“鄆都”疑讀作“壍堵”。

《中國科技史料》2001年第3期刊發了郭書春《〈算數書〉校勘》（簡體排印），^[7]也是釋題名爲“鄆都”，其釋文與整理報告的釋文僅有一處不同，即將“責（積）”徑寫作“積”，並認爲原簡作“責”是訛誤，郭氏在題名“鄆都”下和“積”下分別注曰：

“鄆都”是《九章算術》的“芻甍”。彭文認爲“鄆都”是“壍堵”，未允。^[8]

“積”，原簡訛作“責”，《釋文》校正。^[9]

《內蒙古師大學報》（自然科學漢文版）2001年第3期發表了郭世榮《〈算數書〉勘誤》（簡體排印），^[10]也是釋題名爲“鄆都”，其釋文與整理報告基本相同，祗是將整理報告的“卅（三十）”寫作“卅”、“术（術）”徑寫作“术”，並認爲其图形是“上下倒置的芻甍”，郭文曰：

此題、答、術均正確。但彭文說：“鄆都，疑釋爲“壍堵”。^[11]此說誤。但他所說鄆都的圖形正確。鄆都給出的公式與《九章算術》商功章芻甍術中的公式同，芻甍術曰：“倍下袤，上袤从之，以广乘之，又以高乘之，六而一。”因此，鄆都是上下倒置的芻甍。

《自然科學史研究》2001年第3期發表了鄒大海《出土〈算數書〉初探》（簡體排印），^[12]也是釋題名爲“鄆都”，其釋文與郭世榮完全相同，也是認爲“形狀”與“芻甍同形”，鄒文對題意說明道：

《算數書》的鄆都從音讀上看應爲《九章》的壍堵，^[13]但從形狀上看與壍堵相去甚遠，而與芻甍同形，兩者公式相同但表述不同，術語也有異。

台北《HPM通讯》2002年第2、3期合刊發表了洪萬生、林倉億《〈算數書〉部分題名的再校勘》，^[14]也是釋題名爲“鄆都”，其釋文與郭世榮完全相同，也是認爲其形狀與芻甍相同，該文對題意說明道：

鄆都即《九章算術》中的芻甍。

2004年，[英]古克禮（Christopher Cullen）的著作《中國公元前二世紀數學集〈筭數書〉英譯及注釋》（The Suàn shù shū，筭數書‘Writings on reckoning’:A translation of a Chinese mathematical collection of the second century BC, with explanatory commentary），也將題名寫作“yùn dū鄆都”，並直接英譯爲“wall of Yùn”（鄆之牆），並解釋道：“鄆，山東省的一個古地名，都，可能是‘堵’的借用。”^[15]這顯然是不正确的。

以上諸家的觀點是基本相同的，即一是將《算數書》第143簡算題的名稱隸爲“鄆都”，二是認爲其圖形或同於“壍堵”，或同於“芻甍”。持這類觀點的學界論著還有不少，此不再一一贅述。以上無論是題名的釋讀還是幾何圖形的解讀，均是錯誤的。^[16]

至2006年，對《算數書》第143簡算題的研究有了新的進展，主要表現爲對題名的隸定釋讀和對該題幾何圖形的解讀兩方面。

[日]大阪工業大學張家山漢簡《算數書》研究會《漢簡〈算數書〉——中國最古の數學書》，發現題名當隸定爲“斬都”，原隸定爲“鄆都”誤，爲是。但是，該書又將“斬都”釋爲《九章算術》的“塹堵”，^[17]這是不正確的。

同年，文物出版社出版了整理小組的《張家山漢墓竹簡[二四七號墓]（釋文修訂本）》（以下簡稱《釋文修訂本》），吸收了有關題名隸定的新成果，將“鄆都”改釋爲了“斬都”，爲是，但仍注曰：“斬都，疑讀作‘壍堵’。”^[18]也就是說，仍堅持讀作“壍堵”的觀點。

同年，我們發現該題的幾何圖形是楔口向下、楔口的长度大于与之平行的楔座边的长度的非标准楔形。^[19]之後，我們在不知曉學界改釋“鄆都”爲“斬都”成果的情況下，也發現題名原隸定爲“鄆都”錯誤，當隸爲“斬都”。有關成果曾在2006年10月西南大學主辦的“出土文獻與比較文字學研究博士論壇”上宣讀。^[20]

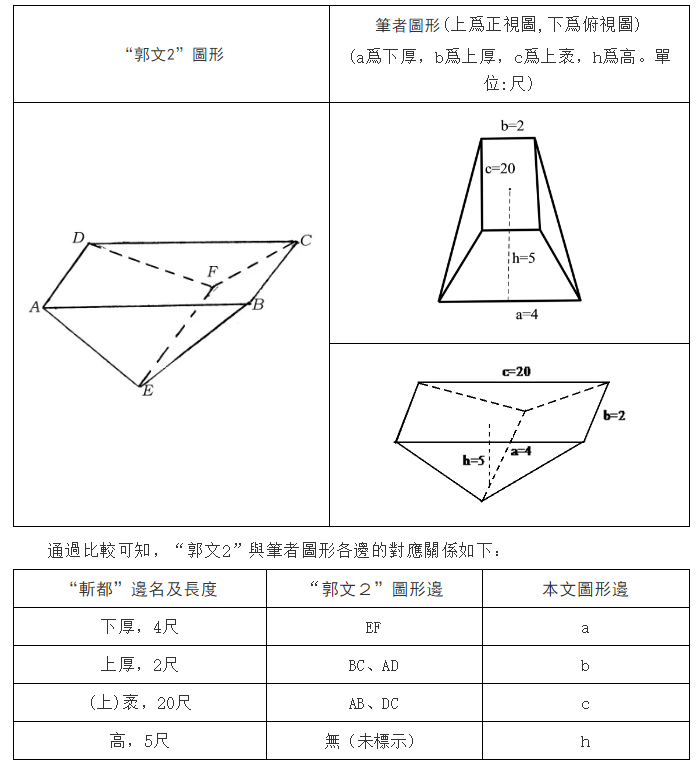
《曲阜師範大學學報》2010年第3期發表了郭書春《〈算數書〉“斬都”求積公式造術初探》（簡體排印。以下簡稱“郭文2”）。^[21]此文吸收了題名改釋“斬都”的成果，並吸收了臺灣清華大學陳良佐關於“斬都”幾何圖形解讀的意見，其圖形如下：^[22]

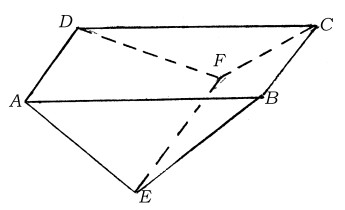
“郭文２”對算題幾何圖形的解讀是正確的，但僅以A、B、C、D、E、F來表示圖形的各角，而圖形中的各邊所代表的是算題中所說的哪條邊（題中有“下厚”“上厚”“高”“袤”諸條邊），不得而知，故其表述還不夠明確而讓人難以理解。

由上可知，張家山漢簡《算數書》第143簡算題研究的新進展有兩個方面，一是在題名上改釋原來的“鄆都”爲“斬都”，二是在幾何圖形上已否定了原來認爲與“芻甍”同形或認爲同於“芻甍”的觀點，這些進展都是可喜的。

但遺憾的是，在學界發表有關以上新成果後，學界仍還有持原有觀點者，主要是國外的有些成果，如：

2008年，[美]道本周（Joseph W. Dauben）的《〈算數書〉英譯及注釋》（算數書Suan Shu Shu A Book onNumbers and Computations，English Translation with Commentary），仍將題名寫作“鄆都”，且給出的幾何圖形也是《九章算術》“壍都”的圖形。^[23]

[法]安立明（Rémi ANICOTTE）的博士論文《從〈算數書〉看中國的計數法與漢語稱數法》（ Nombres et expressions numériques enChine à l’éclairagedes Écritssur les calculs [début du 2e siècleavantnotre ère]）,仍將題名釋爲“鄆都”，也是將幾何圖形解讀爲《九章算術》“壍都”的圖形。^[24]

以上這些成果在新的研究成果已發表後還在持原有觀點，顯然是沒有及時吸收有關成果造成的。

學界有關《算數書》第143簡算題研究的成果較多，以上只是列其代表性者，餘不再贅述。

要真正徹底解決第143簡算題的解讀問題，必須要解決三方面問題：一是題名到底當如何隸定，改釋爲“斬都”是否正確。二是題意（即幾何圖形）到底當怎樣解讀，如“郭文2”那樣解讀是否正確。三是題名的意義是什麽，即得名之由命名之意是什麽，亦即題名是什麽意思，爲什麽要命爲這個名稱。這三方面問題又是相互聯繫的，僅解決其中一方面或兩方面問題，此題的解讀都不算完全徹底，因爲只有這三方面問題都得到解決了，整個算題的問題才算徹底解決了。以下我們就從這三方面來進行論述。

二、題名當釋“斬都”再證

如上所言, 包括整理小組在內的時賢開始都釋題名爲“鄆都”，後來改釋爲了 “斬都”，這是正確的。因爲這一問題非常重要，下面不妨再予以佐證。

遍查《算數書》第143簡以外的所有出土簡帛（楚簡帛、秦簡、兩漢簡帛、三國簡、兩晉簡），均未見“鄆”字，故僅從此點來講，原來隸定爲“鄆都”就非常可疑。

查核圖版可知，原來所謂的“鄆”字實際上是“斬”字。下面是第143簡一開始“斬都”二字的圖版及本文的隸定（見右下）。

此二字未用重文號，故也可說是四字。第二字與第三字間爲編繩處，該書爲先編後寫，故二字間距較大。第一、三字爲同一字，第二、四字爲同一字。

從圖版可清楚看出，第一、三字左邊構件是“車”，不是“軍”。

我們不妨將原簡此四字作一些對比，即可更清楚地說明當釋“斬都”。第二、三字的右邊構件雖不太清晰，^[25]但是第一、四字的右邊構件是很清楚的。通過對比顯然可知，第一、三字與第二、四字的右邊構件是完全不相同的，並非都是“阝（邑）”，第四字及第二字爲“阝（邑）”無疑，而第一字決不是“阝（邑）”，而是“斤”，自然第三字右邊構件也應是“斤”。

通過以上對這四個簡文字形的觀察可知，所謂“鄆都”，實際上是“斬都”。

爲了充分說明釋爲“斬都”的可信性，下面再將第一、三字與同批簡對比。先與同批簡的“斬”字對比：

“斬”字在張家山漢簡共出現34次。通過對比可知，以上所列“斬”字與第143簡第一字寫法均相同，故第一字當釋“斬”。第三字雖右邊不太清晰，既然第一字當釋“斬”，自然第三字也當釋“斬”。

爲了進一步證明第143簡第一、三字的左邊構件是“車”而不是“軍”，下面不妨再將張家山漢簡中的“軍”和从“軍”的“揮”字與之對比：

以下是“軍”字：

“軍”在張家山漢簡共出現50次。通過以上對比可知，這些“軍”字均無第143簡第一、三字所謂“鄆”的左邊寫法。

以下是“揮”字：

“揮”字在張家山漢簡共出現11次。通過以上對比可知，其構件“軍”均無第143簡第一、三字所謂“鄆”的左邊寫法。

下面再將第143簡第一、三字的左邊構件與張家山漢簡中的从“車”的字進行對比，以證明第一、三字左邊構件是“車”：

以下是左邊从“車”的“輒”字：

“輒”字在張家山漢簡共出現14次。通過對比可知，其左邊構件“車”均與第143簡第一、三字的左邊構件相同。

以下是左邊从“車”的“輕”字：

“輕”字在張家山漢簡中共出現8次。通過對比可知，其左邊構件“車”均與第143簡第一、三字的左邊構件相同。

以下是左邊从“車”的“輯”字：

“輯”字在張家山漢簡中共出現3次。通過對比可知，其左邊構件“車”均與第143簡第一、三字的左邊構件相同。

通過以上將第143簡第1、3字的左邊構件與同是張家山漢簡的左邊从“車”的字的對比，也證明第143簡第一、三字左邊構件是“車”而不是“軍”。

以上我們將有關字形作了全面對比，充分說明包括原整理報告在內的題名隸定爲“鄆都”是錯誤的，後改隸爲“斬都”是正確的。

三、“斬都”題意解讀補正

由上可知，包括整理者的原報告、《釋文修訂本》，以及學界不少人，大都認爲143簡算題或與《九章算術》的“芻甍”同形，少部分認爲與“壍堵”同形。這兩種解讀都是錯誤的，實際上，143簡題與“芻甍”和“壍堵”都不同形，是另外一道幾何題。

下面先看《九章算術》的“芻甍”題：

今有芻甍，下廣三丈，袤四丈；上袤二丈，無廣；高一丈。問積幾何？答曰：五千尺。術曰：倍下袤，上袤從之，以廣乘之，又以高乘之，六而一。

根據學界的共識，“芻甍”的形狀屬楔形，其楔口的長度比與之平行的楔座邊的長度短，也就是古時草棚屋頂的形狀，其“屋脊”比與之平行的“屋檐”短。^[26]“上袤二丈”，即楔口（屋脊）的長度爲2丈。“袤四丈”，即與楔口平行的楔座邊（與屋脊平行的那一側屋檐）的長度是4丈；“袤”，指下袤，承前省“下”。“下廣三丈”，即楔座另一條邊（與楔口相鄰的邊，亦即另一側屋檐）的長度是3丈。“無廣”，即“上無廣”，承前省“上”。“高一丈”，即楔座至楔口的高度（屋檐至屋脊的垂直高度）爲1丈。因“上無廣”，故芻甍的形狀是楔形。“芻甍”的形狀如下圖（a爲“上袤”，b爲“下袤”，c爲“下廣”,h爲“高”。單位：尺）：

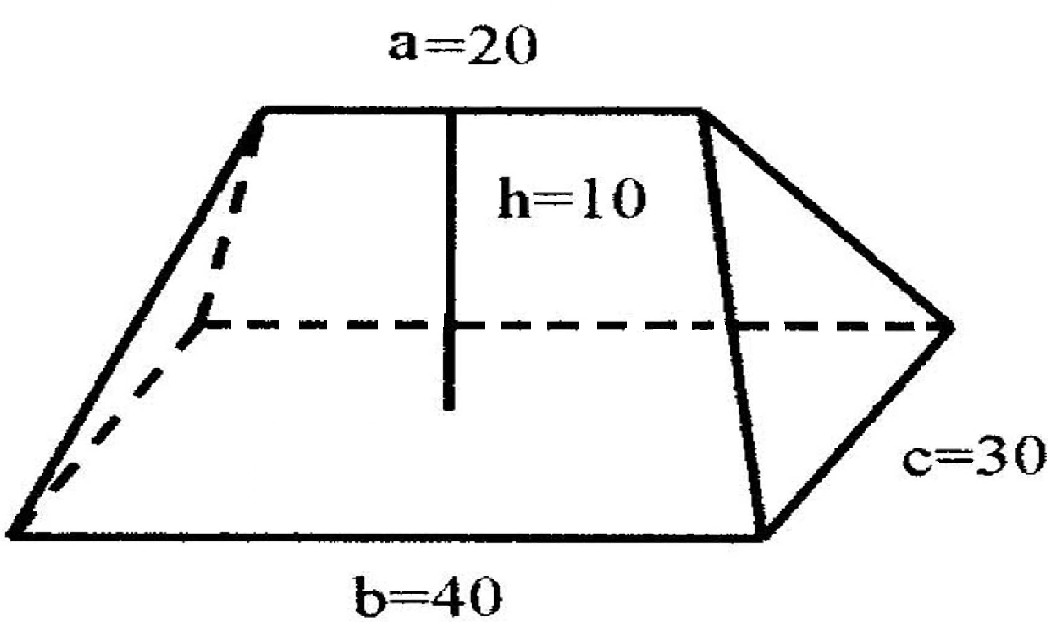
依“芻甍”題給出的演算法（術），該體積求解如下：^[27]

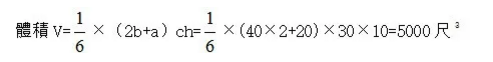
下面再看《九章算术》的“壍堵”题：

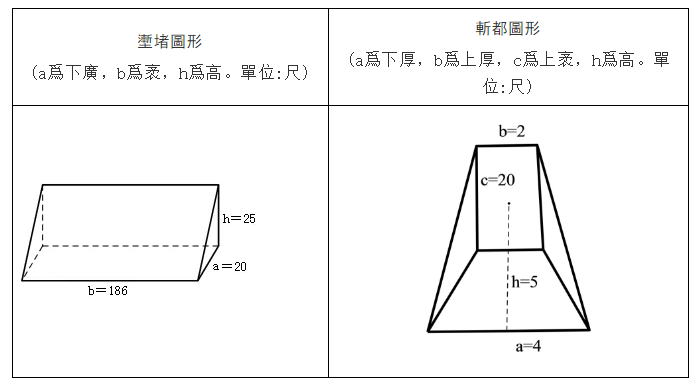
今有壍堵，下廣二丈，袤一十八丈六尺，高二丈五尺，問積幾何？答曰：四萬六千五百尺。

根據學界的共識，“壍堵”的幾何圖形是兩底面爲直角三角形的正柱體，亦即長方體的斜截平分體，其形狀如下圖（a爲下廣，b爲袤，h爲高。單位:尺）：

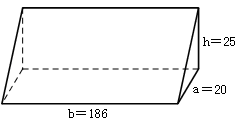
“壍堵”體積求解如下：

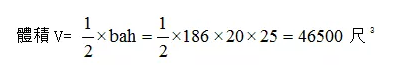
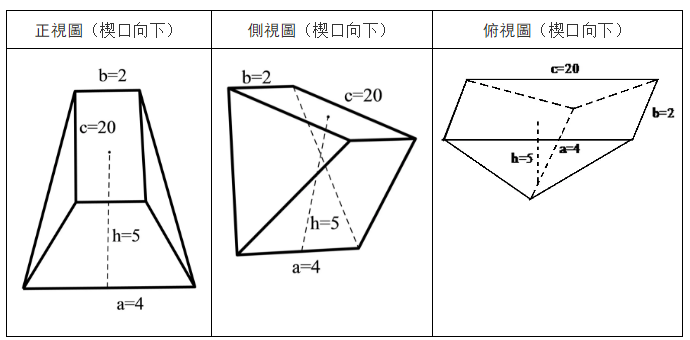
以上是《九章算術》“芻甍”和“壍堵”的題意及其幾何圖形，下面看《算數書》第143簡“斬都”的題意及其幾何圖形。細審該題可知，“斬都”的形狀也屬楔形，但爲非標準楔形，其楔口向下，楔口長度比與楔口平行的楔座邊的長度大（比值爲4：2）、與楔口平行的楔座邊的長度小於相鄰楔座邊的長度（比值爲2:20）。“下厚四尺”，即楔口的長度爲4尺。“上厚二尺”，即與楔口平行的楔座邊的長度爲2尺。“高五尺”，即楔座至楔口的高度爲五尺。“袤二丈”，即“上袤二丈”，亦即楔座的另一條邊的長度爲20尺。還有必要指出的是，“斬都”的“上袤”那一條邊的長度爲20尺，“上厚”的長度爲2尺，這是在解讀“斬都”題意時必須要注意的。

根據題意，“斬都”的圖形如下（a爲下厚，b爲上厚，h爲高，c爲上袤。單位：尺）：

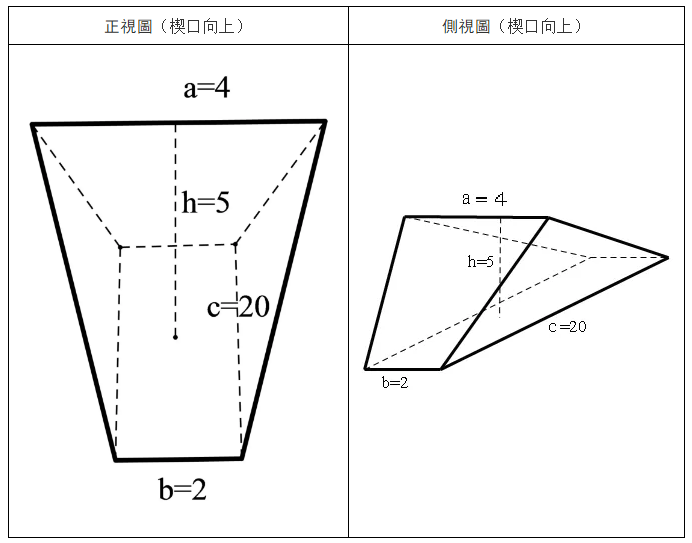
如果將此圖形上下倒置，則爲：

依“斬都”題給出的演算法（術），該體積求解如下：

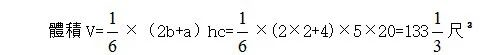
正好與原題答案“責（積）百卅（三十）三尺少半尺”相合。需要說明的是，學界認爲該題的幾何圖形是“芻甍”（上下倒置的芻甍）的觀點是錯誤的。因爲彭浩的觀點是最具代表性且影響最大的，故以下即以之爲例予以說明。彭浩《張家山漢簡〈算數書〉注釋》一書所繪圖形如下^[28]：

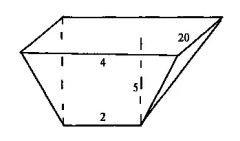
現不妨將彭書圖形與正確圖形作一對比：

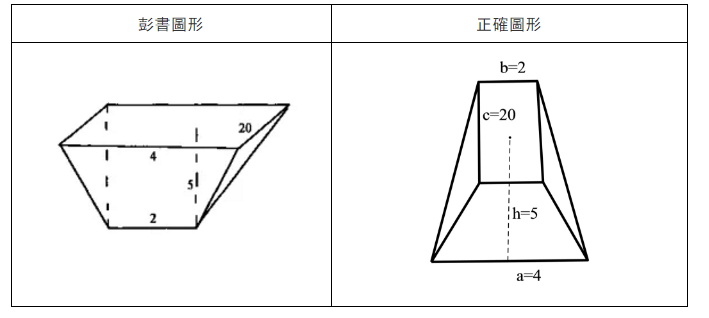通過對比可知，彭書圖形將楔形的楔口和與楔口平行的楔座邊這兩條邊的長度解讀反了，也就是說，彭書將原題的“上厚（2尺）”與“下厚（4尺）”的位置解讀反了，所以描繪出如此錯誤的圖形。彭書所繪圖，實際上是“上厚4尺”、“下厚2尺”。如果按照彭書此圖和給出的各邊長度，則體積爲：

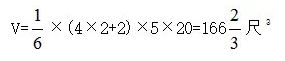
有必要指出的是，“斬都”與“壍堵”雖然語音上關係密切，^[30]但二者所指的幾何圖形是不同的。如前所述，《算數書》“斬都”的幾何圖形是楔口向下、楔口長度比與楔口平行的楔座邊的長度大、與楔口平行的楔座邊的長度小於相鄰楔座邊的長度的非標準楔形。《九章算術》“壍堵”的幾何圖形是兩底面爲直角三角形的正柱體，亦即長方體的斜截平分體。^[31]如上所引整理報告及彭書所注等也發現了將“鄆都”讀作“壍都”在題意上不相合。

如上“一”所述，“郭文2”將斬都的幾何圖形繪爲下圖：

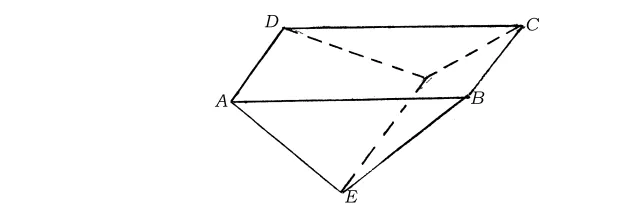
如上所述，“郭文2”對算題幾何圖形的解讀是基本正確的，但僅以A、B、C、D、E、F來表示圖形的各角，而圖形中的各邊所代表的是算題中所說的哪條邊（題中有“下厚”“上厚”“高”“袤”諸條邊），不得而知，故其表述還不夠明確而讓人難以理解。現將“郭文2”的圖形與筆者的圖形對比如下：

通過以上論述可知，“郭文2”對算題幾何圖形的解讀是基本正確的，但“郭文2”圖形意義的表述不太通俗易懂。如果將“郭文2”圖形的表述予以優化，則可表述如下：

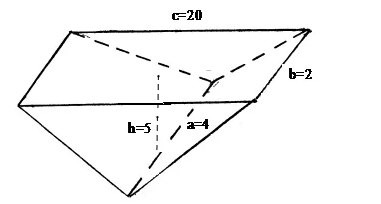
如是，也就通俗易懂了。

嶽麓書院藏秦簡《數》有一道立體幾何算題，編號爲195/0456－196/J13：^[32]

城上廣二丈，下廣五丈，上袤六丈六尺，下毋（無）袤，高六丈四尺，積尺六萬三千三百六十尺。术（術）曰：以上_{（195/0456）}

廣袤相乘，高乘之，二成一尺。_{（196/J13）}

此題寫在兩枚簡上，其中第一枚簡（195/0456）爲整簡，末二字爲“以上”，第二枚簡（196/J13）上端殘約三分之一，甚惜。細審可知，該題的幾何圖形實際上指的是城高低相接過渡處的圖形，且其圖形與“斬都”題圖形是類似的，只是“術”（算法）不同而已。其圖形和算法如下：

正視圖（a爲下廣，b爲上廣，c爲袤6.6，h爲高。單位:丈）：^[33]

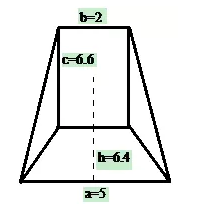
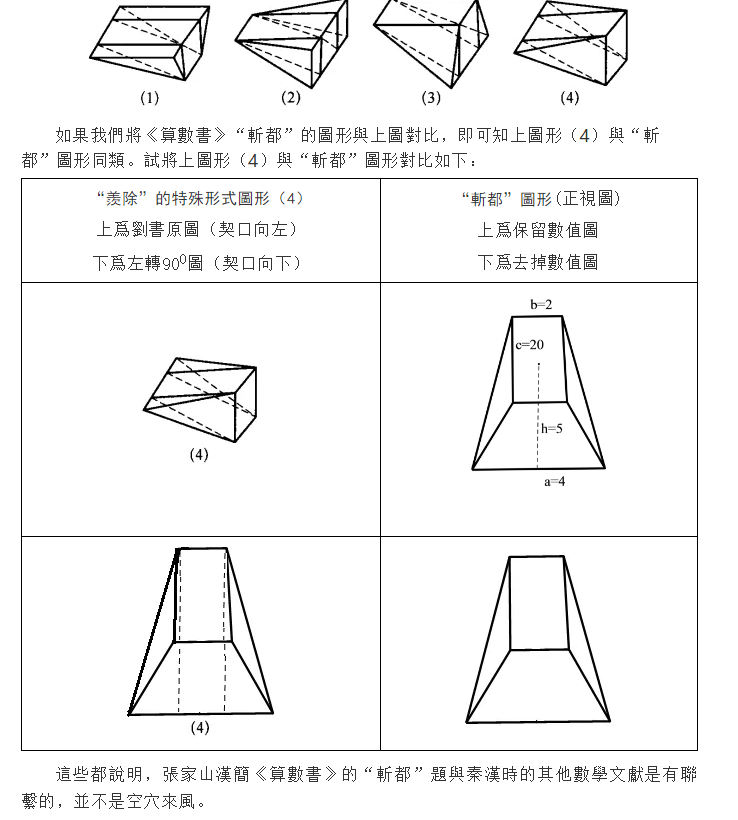
這些都說明，張家山漢簡《算數書》的“斬都”題與秦漢時的其他數學文獻是有聯繫的，並不是空穴來風。

四、“斬都”命名解讀補正

以上論證已說明，包括張家山漢簡整理小組在內的不少時賢對“斬都”題圖形的解讀都不確。“斬都”（即原所謂“鄆都”）並不是《九章算術》的“芻甍”，二者的幾何圖形大不相同，《九章算術》的“芻甍”形狀是楔口向上、楔口長度小於與之平行的楔座邊的長度（比值2:4）、與楔口平行的楔座邊的長度大於相鄰楔座邊的長度（比值4:3）的標準楔形，而《算數書》的“斬都”正相反，是楔口向下、楔口長度大於與之平行的楔座邊的長度（比值4:2）、與楔口平行的楔座邊的長度小於相鄰楔座邊的長度（比值2:20）的非標準楔形。所以，即使將斬都圖形倒置，也絕不類“芻甍”形狀，即絕不類“草棚屋頂的形狀”。“斬都”的幾何圖形也不同于《九章算術》的“壍堵”，因爲“壍堵”是兩底面爲直角三角形的正柱體，亦即長方體的斜截平分體。如果要說張家山漢簡《算數書》的“斬都”，與《九章算術》的“芻甍”和“壍堵”三者的幾何圖形具有什麼共同點的話，那就是三者都可說是楔形；但三者又是不同類型的楔形，絕不是同類幾何圖形。如果要說張家山漢簡《算數書》的“斬都”的圖形與《九章算術》有什麼聯繫的話，倒是可以說與《九章算術》“羨除”的特殊形式圖形之一種相類。

接下來我們必須要解決的問題是，何爲“斬都”呢？此題名的意義是什麽，即得名之由命名之意是什麽，亦即題名是什麽意思，爲什麽要命爲這個名稱，用現代語言學術語來說，就是“斬都”的詞源意義是什麽？且此題名與題意相關嗎？這是我們解讀“斬都”題無法回避的的問題。下面試予以解析。

斬，本指古代的一種刑罰車裂，引申爲砍殺。《說文·車部》：“古用車裂，後人乃法車裂之意而用鈇鉞，故字亦从車。斤者，鈇鉞之類也。”《釋名·釋喪制》：“斫頭曰斬，斬腰曰腰斬。”《周禮·秋官·掌戮》：“（掌戮）掌斬殺賊諜而搏之。”鄭玄注：“斬以鈇鉞，若今要（腰）斬也；殺以刀刃，若今棄市也。”《史記·陳涉世家》：“失期，法皆斬。”再引申爲泛指砍或砍斷。《周禮·考工記·輪人》：“輪人爲輪，斬三材必以其時。”《墨子·非攻下》：“芟刈其禾稼，斬其樹木。”

都，有“橛”義，即“短木樁、木橛子”類義，上古時此義是個方言詞。《方言》卷五：“橛，燕之東北朝鮮洌水之間謂之椴。”郭璞注：“椴，楬杙也，江東呼都。”《廣雅·釋宮》：“椴，杙也。”王念孫疏證：“椴之言段也，今人言木一段兩段是也。”又《釋宮》：“橛，杙也。”王念孫疏證：“凡木形之直而短者謂之橛。”這裏需要注意的是，正如上引郭璞注所說：“椴，楬杙也，江東呼都。”張家山漢簡《算數書》的出土地點正屬於“江東”楚方言區，從此點上講，釋“都”爲“橛”正與郭注相合。^[38]

斬都，即斬削短木樁，砍削木橛子，《算數書》中的算題“斬都”一名自然指砍削短木樁、木橛子而成的楔形，並特指砍削木樁而成的楔口向下、楔口的長度大於與之平行的楔座邊的長度、與楔口平行的楔座邊的長度小於相鄰楔座邊的長度的楔形（屬非標準楔形）。通過以上對該題內容的分析可知，“斬都”所指的幾何圖形正是這種圖形。據此我們可以推測，“斬都”算題是江東的學者對嶽麓書院藏秦簡《數》195/0456－196/J13類算題的發展，幾何圖形未變，只是將“術”（算法）變了的結果。同時，從數學發展史的角度出發，將“斬都”題與嶽麓書院藏秦簡《數》195/0456－196/J13算題、《九章算術》“羨除”算題的特殊形式一並予以考察，可知三者是具有聯繫的，說明“斬都”算題淵源有自，不是空穴來風。

總之，要正確解讀張家山漢簡《算數書》，必須既要重視文字的隸定釋讀，也要重視題意的理解分析，還得重視題名的命名之意的研究，同時注意與同爲上古時期的其他數學文獻一並考察，方才有可能真正弄清楚原書原題的意旨和淵源。當然，這一工作是十分艱難的，不可能一蹴而就，需要學界同仁的長期努力。以上所論，敬請方家指正。

---

附註

[1]原簡寫作“筭數書”。

[2]江陵張家山漢簡整理小組：《江陵張家山漢簡〈算數書〉釋文》，《文物》2000年第9期，第78—84頁；彭浩：《中國最早的數學著作〈算數書〉》，同期85—90頁。

[3]張家山二四七號漢墓竹簡整理小組：《張家山漢墓竹簡[二四七號墓]》，北京:文物出版社,2001。除《算數書》外，該整理報告還同時刊佈了247號墓中的以下以幾種文獻：《曆譜》《二年律令》《奏讞書》《脈書》《蓋廬》《引書》《遣策》。

[4]“袤二丈”後作句號為佳，因後面一句“責（積）百卅（三十）三尺少半尺”是答案，與前面的內容（條件）不同。

[5]“見下圖”，指該書下文所繪圖。關於該圖，下文將有說。

[6]彭浩：《中國最早的數學著作〈算數書〉》，《文物》2000年第9期，89頁。

[7]郭書春：《〈算數書〉校勘》，《中國科技史料》，2001年第3期，202—219頁（以下引文見214頁）。

[8]“彭文”，指彭浩《中國最早的數學著作〈算數書〉》，《文物》2000年第9期85—90。下條所引郭世荣《〈算數書〉勘误》的“彭文”所指同。

[9]郭文的意思是：“積”字，原簡訛作了“責”，《釋文》予以了校正。

[10]郭世榮：《〈算數書〉勘誤》，《內蒙古師大學報》（自然科學漢文版）,2001年第3期，276—285頁（以下引文見283頁）。

[11]此處引用“彭文”不太確，彭浩《中國最早的數學著作〈算數書〉》原文是：“‘鄆都’疑讀作‘壍堵’。”（見上文）且中間沒有逗號。

[12]鄒大海：《出土〈算數書〉初探》，《自然科學史研究》2001年第3期，193—205頁（以下引文見201頁）。

[13]郭文在“壍堵”下注曰：“彭浩先生已說過‘鄆都’疑讀作‘壍堵’。”郭文所引彭浩語指彭浩《中國最早的數學著作〈算數書〉》語。

[14]洪萬生、林倉億：《〈算數書〉部分題名的再校勘》，（臺北）《HPM通訊》2002年第2、3期合刊，6—25頁。

[15]（英）古克禮（Christopher Cullen）：The Suàn shùshū筭數書‘Writings on Reckoning’:A Translation of a Chinese Mathematical Collection of the Second Century BC, with Explanatory Commentary，Needham Research Institute Working Papers, 1，2004,PP.91-93。

[16]下文將會有詳說。

[17]日本張家山漢簡《算數書》研究會：《漢簡〈算數書〉——中國最古の數學書》，日本：朋友書店，2006年，36—37頁。“塹”從“斬”聲，二字古音同；“都”“堵”二字均從“者”聲，二字古音也同，這可能是該書認爲“斬都”就是《九章算術》的“塹堵”的原因。“壍堵”，古籍中又寫作“塹堵”，“壍”“塹”二字爲異體關係。

[18]張家山二四七號漢墓竹簡整理小組：《張家山漢墓竹簡[二四七號墓]》(釋文修訂本)，北京：文物出版社,2006年，151頁。

[19]詳胡憶濤：《張家山漢簡〈算數書〉整理研究》，西南大學碩士論文，2006年5月通過，指導教師張顯成。有關此題的幾何圖形及其解法，下文將有詳述。

[20]在“論壇”上宣讀後，方有與會博士生告之，日本學者已先行改釋爲“斬都”了，可謂不約而同，也感謝相告的博士生！

[21]郭書春：《〈算數書〉“斬都”求積公式造術初探》，《曲阜師範大學學報》，2010年第3期，120—124。這裏簡稱“郭文２”，是與上引郭書春《〈算數書〉校勘》（《中國科技史料》，2001年第3期）相區別。

[22]下圖屬“郭文2”的“圖2”。“郭文2”在列出下圖之前說：“2006年8月洪萬生教授在台北召集的‘《筭數書》及相關簡牘國際研討會’上，學者們就‘斬都’的形狀展開了熱烈討論，但莫衷一是。其中一種意見是‘斬都’爲圖2的形狀，筆者認爲較有道理。近日頃接清華大學（臺灣新竹）陳良佐教授寄來大作《〈筭算數書〉中的體積問題與中國古代體積理論的四個基本原理》，發現其中也將斬都繪成圖2的形狀。”

[23] (美)道本周：（Joseph W.Dauben），算數書Suan Shu Shu A Book on Numbers and Computations，EnglishTranslation with Commentary，Archivefor History of Exact Sciences, 62 (2008)。該題的解讀見155–157頁。

[24]（法）安立明（RémiANICOTTE）， Nombres et expressions numériques en Chine à l’éclairage des Écritssur lescalculs (début du 2e siècleavantnotre ère),法國國立東方語言文化學院博士學位論文，2012年通過，指導教師徐丹。

[25]实际上第二字右边构件“阝（邑）”完全可识。

[26]芻，本指刈草。《說文·艸部》：“芻，刈艸也。象包束艸之形。”漢·袁康《越絕書·外傳記吳王占夢》：“夫越王勾踐雖東僻，亦得系于天皇之位，無罪，而王恒使其芻莖秩馬，比於奴虜。”後泛指喂牲畜的草。《玉篇·艸部》：“芻，茭草。”《孟子·公孫丑下》：“今有受人之牛馬而為之牧之者，則必為之求牧與芻矣；求牧與芻而不得，則反諸其人乎？”甍，屋脊，屋棟。《說文·瓦部》：“甍，屋棟也。”王筠句讀：“此是屋上之長材，椽所憑依者也，今俗謂之屋脊。”《左傳·襄公二十八年》：“猶援廟桷，動於甍。”杜預注：“甍，屋棟。”孔穎達疏：“此是屋上之長材，椽所以馮依者也。今俗謂之屋脊。”所以，芻甍的形狀就是楔口的長度比與之平行的楔座邊的長度短的楔形，有似于古時草棚屋頂的形狀。

[27]有趣的是，現代數學的楔形計算公式與兩千年前的計算公式是相同的，均為：V=（2b+a）ch。

[28]彭浩：《張家山漢簡〈算數書〉注釋》，104頁。順便指出的是，彭書所繪圖形將“袤二丈”（與楔口平行的楔座邊的相鄰邊的長度20尺）那條邊的線段繪得太短，故若僅從所繪圖形來看（而不看標的數字），倒真的是“上下倒置的芻甍”了。

[29]彭浩《中國最早的數學著作〈算數書〉》，《文物》2000年第9期，第89頁。

[30]“斬”為莊母（正齒音）、談部，“壍”為清母（齒頭音）、談部，二者韻同聲相近。“都”與“堵”均端母、魚部，二者音同。故若僅從語音上看，“斬都”與“壍堵”是可相通的。

[31]當然，“壍堵”的幾何圖形也可說是楔形，是楔口長度等同于與之平行的楔座邊的長度的楔形，但它與“斬都”的圖形是不同的，題意自然不同。

[32]“/”前爲整理者據內容編的序號，後爲簡的原始編號。見朱漢民、陳松長主編：《嶽麓書院藏秦簡（貳）》，上海：上海辭書出版社，2011，彩色圖牘見27頁，紅外線圖版見141－142頁。爲便於表述簡文的起迄，隨文標出簡號。

[33]下圖爲正視圖，《嶽麓書院藏秦簡（貳）》第141頁所繪圖爲側視圖。

[34]因該題“術”的簡文已殘不全，現根據所存的“術”殘文，將該題換算成1個“塹堵”和兩個“鱉臑”來計算。

[35]以下見郭書春：《九章筭術譯注》，上海：上海古籍出版社，2009，201頁。筭，今通行寫作“算”，郭書寫作“筭”。

[36]末句的意思是：這是劉徽討論兩廣相等的另外幾種羨除。

[37]以下四種圖形，（1）（3）爲一類，（2）（4）爲一類。

[38]有必要順便指出的是，由於文獻流傳的原因，原來人們未能找到“都”的表示“橛、短木樁、木橛子”義的文獻用例，現出土文獻正好爲我們提供了確切的用例，自然說明出土簡帛文獻在語言文字史研究方面的寶貴價值。

（本文原载《简帛研究》2018年秋冬卷）

张显成，男，1953年生，汉族，成都人。1989年考入四川大学汉语史专业，先后师从经本植教授和赵振铎教授攻读并获得硕士和博士学位。西南大学二级教授、博士生导师，曾任西南大学汉语言文献研究所副所长、所长，现退休返聘。主要从事文献学和语言文字学研究，侧重于简帛和中医文献领域的有关研究；主编《简帛语言文字研究》。完成和正在从事的各级科研和教改项目多项，其中国家社科基金重大项目一项，国家重大文化工程项目1项，国家社科基金一般项目3项，部省级项目9项。获得国家、省部级科研奖和教学奖11项。在中华书局、巴蜀书社、天津古籍出版社、四川大学出版社、西南师范大学出版社等出版著作26部，其中独著10部，主编9部；在海内外发表学术论文100余篇。

马永萍，女，西南大学汉语言文献研究所2016在读博士研究生，导师：张显成教授，研究方向：简帛文献语言文字研究。

胡忆涛，女，西南大学汉语言文献研究所2003级硕士研究生，导师：张显成教授，研究方向：简帛文献语言文字研究。现在连云港市供销合作总社工作。